 |
 |
[Problem noticed by David W. Tamkin ([email protected])]
The problem involves a volume loss in the recorded audio when compared to the original signal (the 'record monitor' output from the MD recorder during recording is normal, it only occurs in the actual audio recorded on the disc).
To investigate the problem I recorded audio from my computer using the digital output on my sound card. By doing this I could ensure that both channels were identical. I used the XMMS audio player's Tone Generator plugin to generate sine waves at desired frequencies. The output from this at maximum volume displayed as 0dB on the Sony MDS-JE520 deck that I used for testing. The sine wave output is useful in this situation because the volume is stable at high frequencies making it easy to notice any volume loss on the level meter of the MD deck.
I set the XMMS plugin to produce 44100Hz 16-bit, Mono audio, which becomes stereo audio with both channels identical during the last stage before being sent to the sound card.
A set of 10 tones was recorded onto a single Minidisc both in monaural and in stereo mode. The stereo recording served as a "control" to ensure that the volume loss was actually being caused by the process of monaural recording rather than by some other factor, such as the ATRAC compression system.
The MD's level meter was used to measure the signal levels. (The sound card cannot be used to check levels since it does not record digitally).
During each recording the level registered on the meter was checked. The tone generator plugin produced all tones at full volume, so the level was 0dB (full) on the meter for all of the frequencies. The frequencies used were 250Hz, and then 1kHz, 2kHz, ... to 20kHz at 1kHz intervals.
Upon playback, all of the stereo recordings registered at full volume on the level meter, meaning no noticeable volume loss was occurring.
The level meter readings during playback of the mono recordings are tabulated below.
Frequency (Hz) Number of Level Meter
bars below 0dB250 0 1000 0 2000 0 3000 0 4000 0 5000 1 6000 1 7000 1 8000 2 9000 2 10000 2 11000 2 12000 3 13000 3 14000 4 15000 5 16000 6 17000 7 18000 7 18500 8 19000 9 20000 10
It should be noted that the level meter scale on the Sony MDS-JE520 deck is not linear. It is marked in decibels from -infinity to 0dB and has 18 bars in this range plus a larger orange bar for 'over' (this bar did not light at any time). The numbers shown in the table above are the number of unlit bars including the 0dB bar.
The observation that no volume loss occurred when the tones were recorded in stereo indicates that the problem lies in the recording of the monaural audio and not in the ATRAC compression, because a similar volume loss would have occurred in stereo mode if that was the case.
The results show a frequency-dependent loss in volume, which increases as the frequency increases.
The use of sine waves in this experiment also allows more general conclusions to be drawn. Fourier's theorem states that any time-varying signal can be decomposed into a sum of sine waves. This means that, as any audio signal can be considered as a combination of sine waves of various frequencies and amplitudes, any signal recorded in mono mode from a source where both channels are identical will be subject to a frequency-dependent loss in volume the same as the one shown in the table above.
When recording a Minidisc in monaural mode from a digital source, the Minidisc recorder must combine the two audio channels transmitted in the SPDIF digital data stream to produce one channel (an SPDIF stream always carries two or four channels of PCM audio data). The 'monauralizing' algorithm is the algorithm used in the DSP chip in the recorder to combine the two audio channels. I suspect that most Minidisc recorders also use the digital 'monauralizing' algorithm to combine the two input channels when recording from analogue sources.
If the signals from the two input channels were out of phase with each other when they were combined, some interference would occur. The loss in amplitude depends on the phase difference. For example, if the phase difference for a particular sine wave is pi radians, or 180 degrees, the two signals cancel out. For general phase differences not equal to integral multiples of 2*pi radians, the combined amplitude is always less than the original. Hence a volume loss will occur if the two identical input channels are out of phase when added together.
As the amount of volume loss increases with increasing frequency, it is clear that the phase difference is increasing with increasing frequency. As my results cover 1-20kHz, the phase difference between the two input channels is increasing over this range. As the volume is never reduced to zero, the phase difference must be less than pi radians for all input frequencies in this range, and it also must be increasing from 1kHz to 20kHz. This type of phase difference could be caused by a synchronisation problem between the two channels on combination.
To illustrate the mathematics behind this, consider combining two identical sine waves of frequency v where one is time shifted by dt relative to the other, causing a frequency-dependent phase shift of 2*pi*v*dt. Then the
output = sin(2*pi*v*t) + sin[2*pi*v*(t+dt)]
which with a bit of trigonometry becomes
output = 2*sin(2*pi*v*t) * cos(pi*v*dt)
The first term in the above is what occurs in the ideal case when there is no phase difference between the left and right signals. The second term is the modulation on the output caused by the phase difference and varies from +1 through to -1 (bear in mind that a change of sign is simply equivalent to an overall phase change of pi). The output is exactly zero when dt = m/(2v) where m is any odd integer ie. for m=1, the first 'zero', v = 1/(2dt).
Instead of using dt we can simply view this as one of the identical channels being some number, a, of sampling intervals, ds, 'behind' the other channel such that dt = a ds. The first 'zero' in the output response will then occur when v = 1/(2*a*ds) = vn/a, where vn = 1/(2ds) is the Nyquist frequency for the signal (equal to 1/2 the sample rate, or alternatively the highest frequency possible to record). If a=1, ie. the left and right channels are 1 sample out of phase (always a good bet for a firmware bug), then the modulation term is cos(pi*v/(2vn)).
In my experiment, the sample frequency was 44100Hz, giving a Nyquist, or maximum signal, frequency of 22.05kHz. If the left and right channels are out of synchronisation by 1 sample then this predicts the output at 22.05kHz would equal 0; would be down by a factor of 2 (6dB) at about 15kHz; 1.32 (2.4 dB) at 10kHz; and only 1.07 (0.6 dB) at 5kHz. Considering the resolution of y of the experiment this prediction agrees amazingly well.
I suspect that the 'monauralizing' process is occurring after the sample rate conversion in most hardware, so the sample frequency would be 44100Hz in all situations.
Because of the good fit with the results of the first experiment detailed above, I decided to retry the experiment with an audio source where the channels were deliberately put out of synchronisation by one sample, to see if I could reverse the suspected problem and successfully record the audio with no volume loss.
To do this I wrote a small C program which takes a monaural 44100Hz 16-bit wave file and produces a stereo file, writing the stereo file out with one channel offset by one sample from the other channel. I then re-ran the experiment detailed earlier, writing the tones to wave files, processing them with the program, and then recording them as before.
As the channels can be offset in either direction, I tried the program, offsetting the channels in both directions, and testing the result with a 16kHz tone. I initially tried it with the left channel one sample behind the right channel. This time the volume loss was greater than before, so I retried it with the left channel one sample in front of the right channel. There was no volume loss!
I re-tested all the frequencies I used in my original experiment from 10-20kHz and none suffered any volume loss with this adjustment.
Sony's 'monauralizing' algorithm has the two audio channels out of synchronisation by one sample when they are combined, such that the sample used from the left channel is one sample earlier than the corresponding sample from the right channel.
When recording mono signals on Sony MD decks the signal level decreases with frequency, as shown in the following figure:
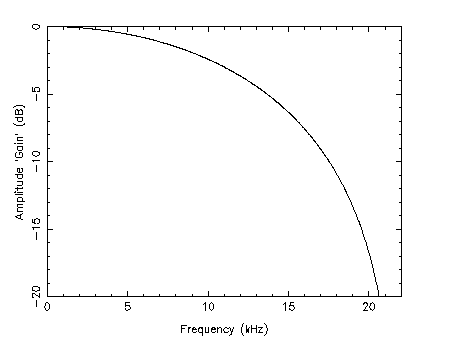 |
| Predicted High Frequency Loss when summing a stereo signal with one sample lag |
The original signal - the volume is full for the first 6 seconds (approx.) and then reduces on the meter gradually, the decrease becomes more rapid at around 16 seconds (it is quite easily noticeable on the level meter).
Left channel has a one sample lag behind the right channel - no reduction in volume.
Right channel has a one sample lag behing the left channel - volume reduces rapidly (much quicker than for testsig.wav) until about 11 seconds, then increases again (the two sample lag means that the frequency for zero volume is 11.025 kHz, as predicted). For 'normal' hardware, testsig.wav would show no volume reduction, and both testsig-lshft.wav and testsig-rshft.wav would show the same reduction as I reported for testsig.wav.